Blaise Pascal was born at Clermont, Auvergne, France on June 19, 1628. He was the son of Étienne Pascal, his father, and Antoinette Bégone, his mother who died when Blaise was only four years old. After her death, his only family was his father and his two sisters, Gilberte, and Jacqueline, both of whom played key roles in Pascal’s life.
When Blaise was seven he moved from Clermont with his father and sisters to Paris. It was at this time that his father began to school his son.  Though being strong intellectually, Blaise had a pathetic physique.
Though being strong intellectually, Blaise had a pathetic physique.
Things went quite well at first for Blaise concerning his schooling. His father was amazed at the ease his son was able to absorb the classical education thrown at him and “tried to hold the boy down to a reasonable pace to avoid injuring his health.” (P 74,Bell) Blaise was exposed to all subjects, all except mathematics, which was taboo. His father forbids this from him in the belief that Blaise was strain his mind. Faced with this opposition, Blaise demanded to know ‘what was mathematics?’ His father told him, “that generally speaking, it was the way of making precise figures and finding the proportions among them.” (P 39,Cole) This set him going and during his play times in this room he figured out ways to draw geometric figures such as perfect circles, and equilateral triangles, all of this he accomplished. Due to the fact that Étienne took such painstaking measures to hide mathematics from Blaise, to the point where he told his friends not to mention math at all around him, Blaise did not know the names to these figures. So he created his own vocab for them, calling a circle a “round” and lines he named “bars”. “After these definitions he made himself axioms, and finally made perfect demonstrations.” (P 39,Cole) His progression was far enough that he reached the 32nd proposition of Euclid’s Book one. Deeply enthralled in this task his father entered the room un-noticed only to observe his son, inventing mathematics. At the age of 13 Étienne began taking Blaise to meetings of mathematicians and scientists which gave Blaise the opportunity to meet with such minds as Descartes and Hobbes. Three years later at the age of 16 Blaise amazed his peers by submitting a paper on conic sections. His sister was quoted as having said “that it was considered so great an intellectual achievement that people have said they have seen nothing as mighty since the time of Archimedes.” (I:Pascal) This was his first real contribution to mathematics, but not his last.
Pascal’s contributions to mathematics from then on were surmising. From a young age he was ‘creating science.’ His first scientific work, an essay on sounds he prepared at a very young age. Once at a dinner party someone tapped a glass with a spoon. Pascal went about the house tapping the china with his fork then disappeared into his room only to emerge hours later having completed a short essay on sound. He used the same approach to all of the problems he encountered; working at them until he was satisfied with his understanding of the problem at hand. A few of his discoveries stood out more than others, of them his calculating machine, and his contributions to combinatorial analysis have made a significant contribution to mathematics.
The mechanical calculator was devised by Pascal in 1642 and was brought to a commercial version in 1645. It was one of the earliest in the history of computing. ‘Side by side in an oblong box were places six small drums, round the upper and lower halves chick the numbers 0 to 9 were written, in descending and ascending orders respectively. According to whichever arithmetical process was currently in use, one half of each drum was shut off from outside view by a sliding metal bar: the upper row of figures was for subtraction, the lower for addition. Below each drum was a wheel consisting of ten (or twenty of twelve) movable spokes inside a fixed rim numbered in ten (or more) equal sections from 0 to 9 etc, rather like a clock face. Wheels and rims were all visible on the box lid, and indeed the numbers to be added or subtracted were fed into the machine by means of the wheels: 4 for instance, being recorded by using a small pin to turn the stoke opposite division 4 as far as a catch positioned close to the outer edge of the box. The procedure for basic arithmetical process then as follows.
To add 315+172, first 315 was recorded on the three (out of six) drums closest to the right-hand side: 5 would appear in the sighting aperture to the extreme right, 1 next to it, and 3 next to that again. To increase by one the number showing in any aperture, it was necessary to turn the appropriate from forward 1/10th of a revolution. Tus in this sum, the drum on the extreme right of the machine would be given two turns, the drum immediately to its left would be moved on 7/10ths of a revolution, whilst the drum to its immediate left would be rotated forward by 1/10th. That total of 487 could then be read off in the appropriate slots. But, easy as this operation was, a problem clearly arose when the numbers to be added together involved totals needing to be carried forward: say 315 + 186. At the periods at which Pascal was working, and because there had been no previous attempt at a calculating-machine capable of carrying column totals forward, this presented a serious technical challenge.(adamson p 23)
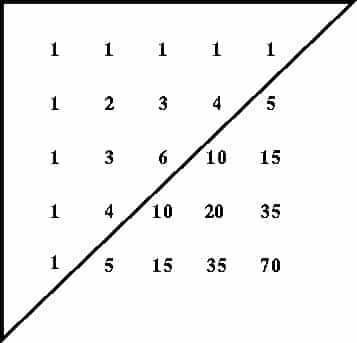
Pascal is also accredited with the advent of Pascal’s triangle; An arrangement of numbers which were originally discovered by the Chinese but named after Pascal due to his further discoveries into the properties which it possessed.
‘Pascal investigated binomial coefficients and laid the foundations of the binomial
theorem.'(adamson p37) ‘A triangular array of numbers consists of ones written on the vertical leg and on the hypotenuse of a right angled isosceles triangle; each other element composing the triangle is the sum of the element directly above it and of the element above it and to the left. Pascal proceeded from this to demonstrate that the numbers in the (n+1)st row are the coefficients in the binomial expansion of (x+y)n. Due to the ease and clarity of the formation of the problems involved, Pascal’s triangle, although not original was one of his finest achievements. It has greatly influenced many discoveries including the theoretical basis of the computer). It has also made an essential contribution to the field of combinatory analysis. It also ‘through the work of John Wallis it led Isaac Newton to the discovery of the binomial theorem for fractional and negative indices, and it was central to Leibniz’s discovery of the calculus.'(adamson p37)
As stated looking closer at the triangle Pascal was able to deduce many properties. First of all, the eateries in any row of the triangle are an equal distance from each other.
He found another property can be derived from the triangle. He discovered that any number in the triangle is the sum of the two numbers directly above it. This was true for triangles, the solved and unsolved. (3/1) + (3/2) = (4/2). Similarly, (5/1) + (5/2) = (6/2). The generalization of this property is known as Pascal’s theorem.
Further studies in hydrodynamics, hydrostatic and atmospheric pressure led Pascal to many discoveries still in use today such as the syringe and hydraulic press. Both these inventions came after years of him experimenting with vacuum tubes. One such experiment was to ‘Take a tube which is curved at its bottom end, sealed at its top end A and open its extremity B. Another tube, a completely straight one open at both extremities M and N, is joined into the curved end of the first tube by its extremity M. Seal B, the opening of the curved end of the first tube, either with your finger or in some other manner and turn the entire apparatus upside down so that, in other words, the two tubes really only consist of one tube, being interconnected. Fill this tube with quicksilver and turn it the right way up again so that A is at the top; then place the end N in a dish full of quicksilver. The whole of the quicksilver in the upper tube will fall down, with the result that it will all recede into the curve unless by any chance part of it also flows through the aperture M into the tube below. But the quicksilver in the lover tube will only partially subside as part of it will also remain suspended at a height of 26′-27’ according to the place and weather conditions in which the experiment is being carried out.
The reason for this difference is because the air weights down on the quicksilver in the dish beneath the lower tube, and thus the quicksilver which is inside that tube is held suspended in balance.
But it does not weigh down upon the quicksilver at the curved end of the upper tube, for the finger or bladder sealing this prevents any access to it, so that, as no air is pressing down at this point, the quicksilver in the upper tube drops freely because there is nothing to hold it up or to resist its fall.
All of these contributions have made a lasting impact of all of mankind. Everything that Pascal created is still in use today in some way or another. His primitive form of a syringe is still used in the medical field today to administer drugs and remove blood. The work he did on combinatory mathematics can be applied by anyone to ‘figure out the odds’ concerning a situation, which is exactly how he used it; by going to casinos and playing games smart. Something that anyone can do today. The work he did concerning hydraulic presses are still in use today in factories, and car garages.