Zeno of Elea was born in Elea, Italy, in 490 B.C. He died there in 430 B.C., in an attempt to oust the city’s tyrant. He was a noted pupil of 
Parmenides, from whom he learned most of his doctrines and political ideas. He believed that what exists is one, permanent, and unchanging. Zeno argued against multiplicity and motion. He did so by showing the contradictions that result from assuming that they were real. His argument against multiplicity stated that if the many exists, it must be both infinitely large and infinitely small, and it must be both limited and unlimited in number. His argument against motion is characterized by two famous illustrations: the flying arrow, and the runner in the race. It is the illustration with the runner that is associated the first part of the assignment.
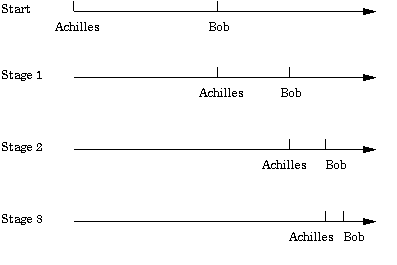
In this illustration, Zeno argued that a runner can never reach the end of a race course. He stated that the runner first completes half of the race course, and then half of the remaining distance, and will continue to do so for infinity. In this way, the runner can never reach the end of the course, as it would be infinitely long, much as the semester would be infinitely long if we completed half, and then half the remainder, ad infinitum. This interval will shrink infinitely, but never quite disappear. This type of argument may be called the antinonomy of infinite divisibility, and was part of the dialectic which Zeno invented. These are only a small part of Zeno’s arguments, however. He is believed to have devised at least forty arguments, eight of which have survived until the present. While these arguments seems simple, they have managed to raise a number of profound philosophical and scientific questions about space, time, and infinity, throughout history. These issues still interest philosophers and scientists today.
The problem with both Zeno’s argument and yours is that neither of you deal with adding the infinite. Your argument suggests that if one adds the infinite, the sum will be infinity, which is not the case. If the numbers are shrinking infinitely at the same rate, then eventually they will equal a certain number, not infinity as both Zeno’s argument and yours suggest. A simpler way to explain this would be to say that if the first half of the semester takes a certain amount of time, and time always passes at the same rate, then the second half of the semester will also take a certain amount of time, which can be measured.
