Fluid: system that yield to any force that attempts to alter their shape, causing system to flow until it reaches mechanical equilibrium; fluid conforms to shape of container
Molecules of liquid in condense state; maintain CONSTANT intermolecular distance. Liquid will form SURFACE. Gas will not form surface; adjust intermolecular distance to fill space provided (compression/ expansion)
Fluid in mechanical equilibrium; fluid= stationary
Equilibrium: state in which all essential parameter of system are TIME-INDEPENDENT; no observable change while you observe system
Ideal Stationary Fluid:
- Incompressible; volume & density remain constant (applies for liquids and IDEAL gases, not real gases)
- Deformable; under the influence of forces and
- Seeks a mechanical equilibrium
- Once mechanical equilibrium is reached; fluid= stationary (apples to both liquids & gases)
Consequence: Density= CONSTANT
Pascal’s Law
- Pressure of ideal fluid varies with vertical distance
- Take a fluid block, tiny, able to locate, define as (bottom: y1 top: y1 + dY) (Fnet,y= 0= Fup-(W+Fdown)
The difference between the pressures at two different positions in a fluid is proportional to the vertical distance between these two positions. The proportionality factor is the produce of the density of the fluid and the gravitational acceleration
|W|= g x dn= density x gravity x Area x dY
- P2-P1= -density x gravity (Y2-Y1) * General Form (pressure change is linearly proportional to change in Y value) used when the surface of the fluid can’t be identified for a reference point (i.e blood in veins) as you go down (increase Y, you will increase P)
- P (ymax)=0= Patm + density x gravity x depth (in atm)*Used when surface is found; express it as pressure at surface + weight of water column above depth (identify surface of fluid toward ambient atmosphere or a vacuum due to mechanical equilibrium between air pushing down on water and water pushing up
- Convert Density into kg/m^3. ON EARTH!
- Pascal Law doesn’t apply to fluid air (can’t explain pressure variation in atmosphere)
- Atmosphere is NOT a stationary fluid because density is NOT constant
- Doesn’t apply to gases because gases are compressible and their density depends on pressure.
- Pascal’s law doesn’t explain shape of container; Pressure increases below surface to given fixed value at any given depth; regardless of container shape.
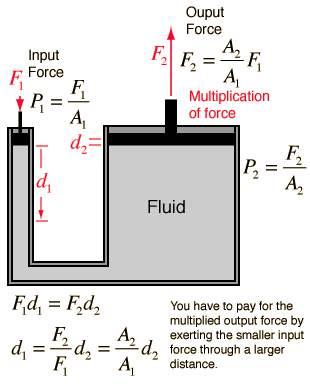
P1 = P2 (since the pressures are equal throughout).
F1/A1 = F2/A2 ——– P=F/A
V1 = V2 (fluid pushed down on the left side equals the volume of fluid that is lifted up on the right side, the following formula is also true.)
Blood Pressure
- Blood pressure is a gauge pressure (unlike absolute pressure, gauge pressure can be -/+) (pblood= pabsolute – patm) (pressure relative to air pressure that varies throughout the cardiovascular system
- If we had negative gauge pressure in blood vessel, it would collapse; though values are below (0), pressure in blood is not below 1 atm (negative gauge pressure, a way of expressing pressure measurements below atmospheric pressure)
- For measurements in blood use general formula: P2-P1= density x gravity (Y2-Y1)
∆p= densityblood x g x ∆y (if (-) it means the change from the heart to the brain. So heart pressure- (calculated pressure) = pressure in brain
∆p= pressure change from heart to brain
∆y based on vertically y-axis pointing upward
In blood the pressure at the heart becomes the atmospheric pressure [gauge= abs = heart pressure]
- High: found in aorta, arteries, arterioles, capillaries
- Diastolic (80mmHg (10.7kpa) – Systolic (120mmHg (16.0kpa)
- Low: veins, pulmonary circulation
- Cardiovascular system will exceed ambient air pressure everywhere ONLY WHEN LYING DOWN
- Taller animals will have higher systolic blood pressure in order to compensate for having to pump blood farther around the body
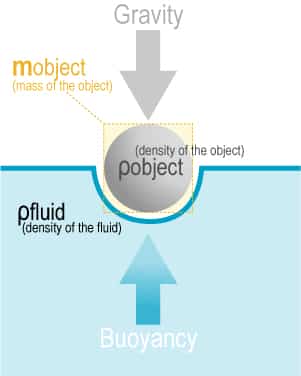
Buoyancy (Archimedes Principle)
- Buoyancy: an upward acting force exerted by a fluid, which opposes an object’s weight. (Buoyancy = weight of
 displaced fluid.)
displaced fluid.) - If the object is either less dense than the liquid or is shaped appropriately (as in a boat), the force can keep the object afloat.
- Archimedes’ principle does not consider the surface tension (capillarity) acting on the body.
- When at mechanical equilibrium (Fup-Fdown-Wf= 0)
- However the (Fup-Fdown= Wf > 0)
- Fnet>0= weight of block is less than weight of displaced fluid, air bubbles (block B) rises to the top
- Fnet=0 Block will float at its current depth
- Fnet<0 weight of block is greater than the weight of the displaced fluid and the block will sink to the bottom of the container.
- Archimedes principle: When an object is immersed in a fluid, the fluid exerts an upward force on the object equal to the weight of the fluid displaced by the object.
Pbuoyant= Densityfluid x Volumeobject x gravity (replaced Wf not Fnet)
- Buoyant force is ALWAYS directed upward (opposite of gravity) (as volume increase, buoyant forces increase) **if all other parameters are kept equal
- Whether something floats or sinks is NOT determined by weight but by its density/ volume relative to the density of the surrounding fluid.
- Having salt water can vary the density of the liquid as compared to fresh water. The weight of the water INCREASES as the salt content increases.
- ‘Buoyancy force in air = weight of object in empty space – weight of object immersed in fluid’
Suppose a rock’s weight is measured as 10 newtons when suspended by a string in a vacuum with gravity acting upon it. Suppose that when the rock is lowered into water, it displaces water of weight 3 newtons. The force it then exerts on the string from which it hangs would be 10 newtons minus the 3 newtons of buoyant force: 10 − 3 = 7 newtons.
