Introduction
In the study of physics, velocity is defined as the rate of change in position in accordance to a reference point. It is therefore a vector quantity; both the scalar quantities of speed and direction are required to define it. In the SI system, it is measured in meters per second: (m/s) [N] meaning the scalar value of velocity is speed. For example, “15 meters per second” is a scalar, whereas “15 meters per second east” is a vector. The average velocity of an object moving with direction and magnitude during a time interval (Δt) is described by the formula:
Purpose
To determine the relationship (if any) between the slope of a position-time graph and velocity.
Materials and Method
Materials:
– Masking Tape
– Metre Stick
– Stop Watch
– School Accessories
Variables:
Independent: The velocity being travelled by the walker
Dependent: The average velocity
Controlled: The 10m course, the timer, the walker, the recorder, test environment, interval measurements
Method
1) All materials were collected and taken to the testing station.
2) Using masking tape a 10 meter circuit was created in the hallway. Every meter was indicated with a strip of tape and every two meters were indicated with an “x”.
3) A recorder, timer and walker were all designated and kept constant throughout the course of the experiment.
4) Part A of the experiment was performed. The data was recorded. (Move Forward with a slow constant velocity throughout the trip)
5) Part B of the experiment was performed. The data was recorded. (Repeat a, but move forward at a constant fast velocity)
6) Part C of the experiment was performed. The data was recorded. (Move forward at a slow constant velocity for 3m. Stop 5s. Then move forward at a constant fast velocity)
7) Part D of the experiment was performed. The data was recorded. (Move forward at a slow constant velocity for 3m. Stop for 5s. Then move forward with a faster constant velocity to the farthest position. Stop for 10s. Then return to the starting point with a medium constant velocity.)
8) Once the testing was complete all materials were collected and the test station was cleaned up.
Observations
| Trip A | |
| Time (s) Uncertainty: +/-.05ms | Position (m) [S] Uncertainty: +/- .05mm |
| 0.00 | 0.00 |
| 2.53 | 2.00 |
| 4.75 | 4.00 |
| 6.99 | 6.00 |
| 9.57 | 8.00 |
| 12.08 | 10.00 |
| Trip B | |
| Time (s) Uncertainty: +/-.05ms | Position (m) [S] Uncertainty: +/- .05mm |
| 0.00 | 0.00 |
| 2.11 | 2.00 |
| 3.92 | 4.00 |
| 4.87 | 6.00 |
| 6.15 | 8.00 |
| 8.34 | 10.00 |
| Trip C | |
| Time (s) Uncertainty: +/-.05ms | Position (m) [S] Uncertainty: +/- .05mm |
| 0.00 | 0.00 |
| 2.83 | 2.00 |
| 4.91 | 4.00 |
| 11.94 | 6.00 |
| 13.46 | 8.00 |
| 14.87 | 10.00 |
| Trip D | |
| Time (s) Uncertainty: +/-.05ms | Position (m) [S] Uncertainty: +/- .05mm |
| 0.00 | 0.00 |
| 2.93 | 2.00 |
| 9.14 | 4.00 |
| 10.35 | 6.00 |
| 12.63 | 8.00 |
| 14.67 | 10.00 |
| 25.89 | 8.00 |
| 27.31 | 6.00 |
| 29.21 | 4.00 |
| 32.16 | 2.00 |
| 33.82 | 0.00 |
Calculations
Trip A
| —
Vav=d ₁ ∆t |
_
Vav=d₂ ∆t |
_
Vav=d₃ ∆t |
_
Vav=d₄ ∆t |
_
Vav=d₅ ∆t |
| _
Vav= 2.00m/s [S] 2.53s |
_
Vav= 2.00m/s [S] 2.22s |
_
Vav= 2.00m/s [S] 2.24s |
_
Vav= 2.00m/s [S] 2.58s |
_
Vav= 2.00m/s [S] 2.51s |
| _
Vav= .8m/s [S] |
_
Vav= .9m/s [S] |
_
Vav= .9m/s [S] |
_
Vav= .8m/s [S] |
_
Vav= .8m/s [S] |
| Total Average Velocity | (10m [S])/ 12.08)= .8m/s [S] | |||
Trip B
| —
Vav=d ₁ ∆t |
_
Vav=d₂ ∆t |
_
Vav=d₃ ∆t |
_
Vav=d₄ ∆t |
_
Vav=d₅ ∆t |
| _
Vav= 2.00m/s [S] 2.11s |
_
Vav= 2.00m/s [S] 1.81s |
_
Vav= 2.00m/s [S] 0 .95s |
_
Vav= 2.00m/s [S] 1.28s |
_
Vav= 2.00m/s [S] 2.19s |
| _
Vav= 1 m/s [S] |
_
Vav= 1 m/s [S] |
_
Vav= 2 m/s [S] |
_
Vav= 2 m/s [S] |
_
Vav= .9m/s [S] |
| Total Average Velocity | (10m [S])/ 8.34)= 1 m/s [S] | |||
Trip C
| —
Vav=d ₁ ∆t |
_
Vav=d₂ ∆t |
_
Vav=d₃ ∆t |
_
Vav=d₄ ∆t |
_
Vav=d₅ ∆t |
| _
Vav= 2.00m/s [S] 2.83s |
_
Vav= 2.00m/s [S] 2.08s |
_
Vav= 2.00m/s [S] 7 .03s |
_
Vav= 2.00m/s [S] 1.52s |
_
Vav= 2.00m/s [S] 1.41s |
| _
Vav= .7 m/s [S] |
_
Vav= 1 m/s [S] |
_
Vav= .3 m/s [S] |
_
Vav= 1 m/s [S] |
_
Vav= 1m/s [S] |
| Total Average Velocity | (10m [S])/ 14.87)= .7 m/s [S] | |||
Trip D
| —
Vav=d ₁ ∆t |
_
Vav=d₂ ∆t |
_
Vav=d₃ ∆t |
_
Vav=d₄ ∆t |
_
Vav=d₅ ∆t |
| _
Vav= 2.00m/s [S] 2.93s |
_
Vav= 2.00m/s [S] 6.21s |
_
Vav= 2.00m/s [S] 1.21s |
_
Vav= 2.00m/s [S] 2.28s |
_
Vav= 2.00m/s [S] 2.04s |
| _
Vav= .7 m/s [S] |
_
Vav= .3 m/s [S] |
_
Vav= 2 m/s [S] |
_
Vav= .9 m/s [S] |
_
Vav= 1m/s [S] |
| —
Vav=d₆ ∆t |
_
Vav=d₇ ∆t |
_
Vav=d₈ ∆t |
_
Vav=d₉ ∆t |
_
Vav=d₁₀ ∆t |
| _
Vav= 2.00m/s [S] 11.22s |
_
Vav= 2.00m/s [S] 1.42s |
_
Vav= 2.00m/s [S] 7 .03s |
_
Vav= 2.00m/s [S] 1.52s |
_
Vav= 2.00m/s [S] 1.9s |
| _
Vav= .2 m/s [S] |
_
Vav= 1 m/s [S] |
_
Vav= .3 m/s [S] |
_
Vav= 1 m/s [S] |
_
Vav= 1m/s [S] |
| Total Average Velocity | (20m [S])/ 33.82)= .4 m/s [S] | |||
Error Analysis
Trip A
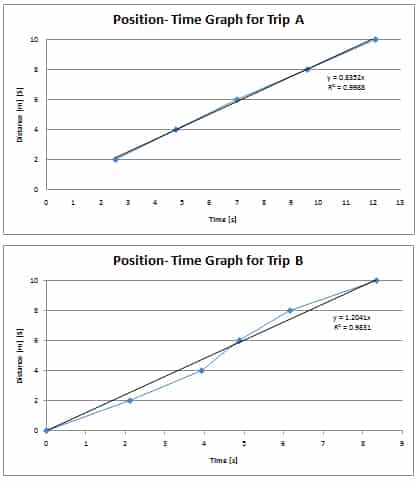
The R² value was = 0.9988 which is only .0012 of from a linear relationship. (Constant velocity)
Trip B
The R² value = 0.9831 which is .00169 of from a linear relationship. (Constant velocity)
Trip C
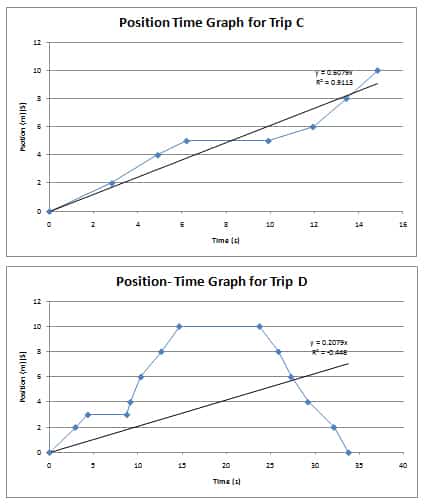
The R² value = 0.948 which is .0052 of from a linear relationship. (Constant velocity)
Trip D
Method DR² value = -0.371 which is .629 of from a linear relationship. (Constant velocity)
Human Error: During the experiment there were two primary sources of human error, the walker and timer. The walker’s pace was not consistent throughout the entire 10m circuit due to different aspects such as having to stop or trying to maintain a constant fast or slow pace. This resulted in there being different average velocities for each interval even when the average velocity was supposed to be constant. The timer was recording the walker’s distance at every two meter interval however the walker did not stop at all during the 10 metre circuit. This resulted in the timer having to use their own digression to decide when exact the walker crossed each 2m mark and to make sure the times were accurate with what was actually occurring.
Equipment Error: Measurement Uncertainty: Timer +/- .05ms , Meter Stick +/- .05mm. Both of these uncertainties in the measuring devices could potentially have resulted in one interval being longer than another or the velocity of one interval bring slightly faster or slower than another.
Discussion Questions
1) Trip A and B was relevantly the same. The only difference between the two was the velocity travelled during each trip. Both resulted in a near constant velocity throughout the duration of the trip. Trip C had the addition of stopping which meant one velocity in the trip being extremely slow in comparison to the others. Trip D was unique because it incorporated both the stopping of the walker and the return of the walker to the reference point, which meant a negative slope.
2) Positive Slope= This means the walker was moving away from the reference point. The more linear the slope is, the faster the person is moving.
3) Negative Slope= This means the walker is moving back to the reference point. The more linear the slope is, the faster the person is moving.
No Slope= This means the walker was not moving.
4) The two primary errors during the experiment were making sure the walker was moving at a constant pace and that the timer was getting the correct times for each intervals. The problem of the person moving at a constant rate could have been minimized through setting stricter guidelines for the person, such as counting out their paces or removing the human element all together and using a machine. The timing problem could be fixed by using the “lap” function next time or perhaps using a timer at each interval which is stopped by the person stepping on the tape.
Conclusion
The purpose of this lab was to find the relationship between the slope of the line of best fit and the average velocity. Each graph has a y=x value above its R² value which indicated the slope of the line. If this slope value is compared to the calculated average velocity data of each trip, the values are almost identical. This proves that the slope of the line of best fit is actually the average velocity of each trip. If the slope of each individual line segment was measured, the data would match the values of each time intervals’ calculated average velocity. The data for the most part was not surprising and relatively precise but there is always room for improvement.