1. AIM/ PURPOSE:
The aim of this experiment is pretty simple. It is to measure the refractive index of the light while it moves from one medium to another. Depending on the refractive indexes of both mediums, the angle of refraction will be at a greater or lesser angle. The angles are measured from the normal line, which is the line perpendicular to the meeting of both mediums. How to find the refraction index? There is a formula: n=c/v (which is speed of light in vacuum/ speed of light in material). In our example of water and air, the light would refract away from the normal line. This occurs because of water slowing down the light, and this would cause the light to be bended which is equal to refraction. This can be verified by the use of Snell’s law which states that incident ray, refracted ray and normal line are all lying on the same plane. Snell’s law has a formula: sin(i)/sin(r). To test and prove our hypothesis/theory we will fill up the container halfway with water, use a laser as a source of light and measure the angles. After the formula is applied we will be left with pretty accurate results.
2. RESEARCH QUESTION:
How to find/measure the refractive index of the material (in this case water and oil)? How are angles i (incident) and r (refractive) related? How to apply Snell’s law?
3. INTRODUCTION:
A container/ tank in a circular shape with angles is filled up halfway with a material (water and oil).
4. HYPOTHESIS/ PREDICTIONS:
Water’s refractive index will be equal to 1.333. We will also make a graph and a table.
5. PROCEDURE (DESCRIPTION OF THE EXPERIMENT):
We started with choosing a suitable circular container with angles which is used for refraction and filling it up with water. For the other container, we did the exact same thing but with oil. We connected the laser so that it was pointing right in the center and from different angles. Our tutor also mentioned that pointing the laser from beneath the container would give the same results, so we decided to examine that too. We took notes of the results. We found sin(i) and sin(r) separately. Then we divided them and got n (the refraction index). I then made a graph knowing that the slope=rise/rum=sin(i)/sin(r)=n. Units are very important in physics, but at the moment, in this experiment, the refractive index does not have a unit.
6. DATA AND ANALYSIS:
- Tools used: laser, laser refraction tank(a container with angles), scientific/ graphic calculator.
- The picture of the experiment and the tools:

- Data organized in a table:
| # | i (incident angle) | r (refractive angle) | sin (i) | sin (r) | refractive index (n) |
| 1 | 10 | 7 | 0.174 | 0.122 | 1.4 |
| 2 | 20 | 15 | 0.342 | 0.259 | 1.3 |
| 3 | 30 | 21 | 0.5 | 0.358 | 1.4 |
| 4 | 40 | 29 | 0.643 | 0.485 | 1.3 |
| 5 | 50 | 36 | 0.766 | 0.588 | 1.3 |
| 6 | 60 | 41 | 0.866 | 0.656 | 1.3 |
| 7 | 70 | 45 | 0.94 | 0.707 | 1.3 |
| 8 | 80 | 48 | 0.985 | 0.743 | 1.3 |
- The calculations: Find the refractive angles
- Find sin (i) with a calculator
- Find sin (r) with a calculator
Divide the results in sin(i) by sin(r) and get the refractive index
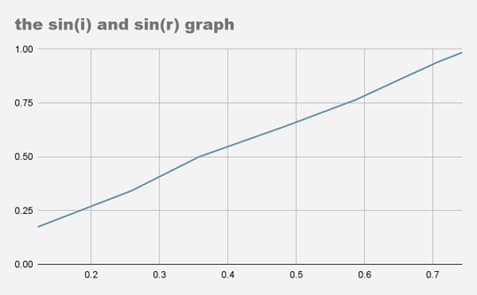
The y-axis of the graph is sin (i). The x-axis of the graph is sin (r). How did I create the graph? I inserted my results from the table and applied them in google sheets. There is a formula for the slope or gradient of the graph, which is rise/rum; knowing that sin(i)/sin(r) is equal to that, we can find and draw the graph using the results.
Absolute uncertainty:
Formula- 𝚫x= (xmax- xmin)/2
Formula- xav= add all numbers and divide them by the number of numbers
sin(i)av=(0.174+0.342+0.5+0.643+0.766+0.866+0.94+0.985)/8≈ 0.652
sin(r)av=(0.122+0.259+0.358+0.485+0.588+0.656+0.707+0.743)/8≈ 0.490
nav=(1.4+1.3+1.4+1.3+1.3+1.3+1.3+1.3)/8≈ 1.33
𝚫sin(i)→(0.985-0.174)/2= 0.4055 0.652 ± 0.406
𝚫sin(r)→(0.743-0.122)/2=0.3105 0.490 ± 0.311
𝚫n→(1.4-1.3)/2=0.05 1.33 ± 0.05
Fractional uncertainty:
0.406/0.652≈0.623
0.311/0.490≈0.635
0.05/1.33≈0.0376
Percentages uncertainty:
0.623×100%= 62.3%
0.635×100%= 63.5%
0.0376×100%= 3.76%
7. CONCLUSION AND EVALUATION:
Our hypothesis was proven to be correct. To conclude, we used formulas: sin(i)/sin(r) and rise/rum. It was very informative and taught us a lot. This is one of the foundation topics in the world of physics. The experiment was successful. We calculated the absolute uncertainty as in the last experiment. We found the refractive index, which is approximately 1.3 on average. We also made a graph using the table with the results.
