ASCII: American Standard Code for Information Interchange

• Recall: Computers communicate using binary
• Therefore, computers do NOT process information using characters (e.g. letters).
• Each letter or character has a number representation that the computer uses to refer to the character.
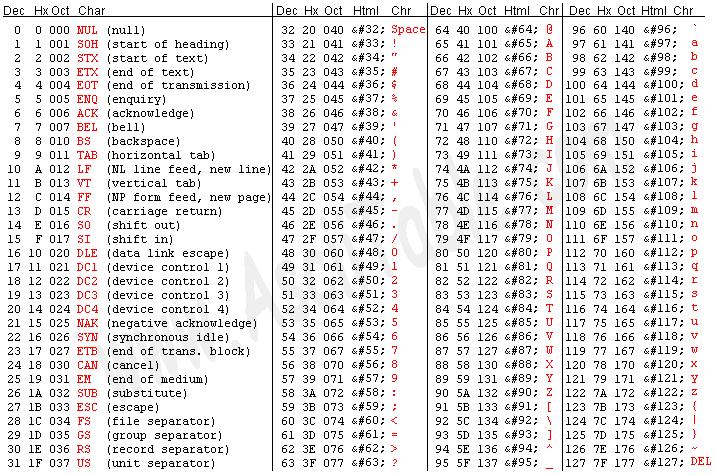
• ASCII: American Standard Code for Information Interchange
• ASCII is a code for representing English characters as numbers.
• The ASCII numbers range from 0 to 255, each representing a character.
• Numbers 0-32 are set aside for communications and printer control
• Numbers 33-127  are standard characters
• Numbers 128-255 are “extended” characters, or those not found on the keyboard.
• Humans process information in decimal and ASCII
• Therefore, when communicating with a computer, the computer will translate the information from ASCII to binary for us! (and also binary to ASCII)
• Recall
• When converting binary to decimal, binary numbers have a place value of base 2.
• That is

• ^· 2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰

• ^{o or}

• ^{· 128                  64                    32                    16                    8                     4                     2                     1}

• Recall:
• Convert the following binary numbers to decimal numbers

• 00000101
• 00001000
• 01110101
• 01010001

• Notice: All the binary numbers are 8 digits long.

• Each byte in memory can hold an ASCII character.
• Each byte holds 8 bits
• Each bit can be represented by a 1 or 0

• Therefore, each byte can hold an ASCII character that is composed of 8 bits.

• Recall: Memory can be thought of an array of boxes that holds a single byte of information.

• Solve:
• Convert the following binary numbers to ASCII characters
• 0111010101010001

• Solution:
• Step 1:
  • Break apart the sequence into 8 bit (1 byte) sections to decode
  • 111010101010001=1110101 and 0101000

• Note: because 1110101 is seven digits and eight is needed, simply add a 0 to the front: 01110101

• Step 2:
  • Convert each 8 bit sections to decimal numbers
    • 01110101 =  117
    • 01010001 =   81

• Step 3:
  • Convert decimals to ASCII characters (by looking it up to the table)
    • 117 = u
    • 81 = Q

• Therefore, 0111010101010001 = uQ

Recall:

• The ASCII representation for the letter ‘w’ is 119₁₀. What is the ASCII representation for the letter ‘w’ in binary form?